Section outline

  • TABLEAUX - GRAPHIQUES CROISES DYNAMIQUES - OLAP

    Collapse all Expand all

    A. TABLEAUX CROISES DYNAMIQUES

    Les tableaux croisés offrent une présentation synthétique des données d'une liste Excel ou d'une base externe, en fonction des critères choisis par l'utilisateur.

    1.CRÉATION AUTOMATIQUE

    Des tableaux tout faits sont proposés.

     onglet "insertion"
    groupe "tableaux"     (1er bloc)
    une cellule de données du tableau étant sélectionnée
    <clic g>     sur
    dans le volet de gauche
    sélectionner le modèle désiré
    il s'affiche dans le volet de droite
     pour valider
    il s'affiche dans une nouvelle feuille de travail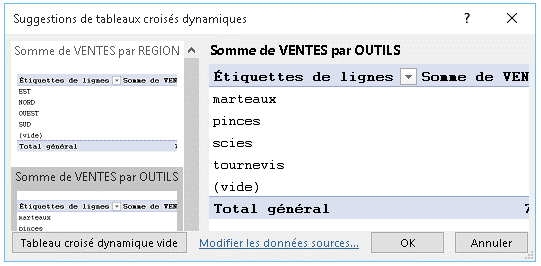

     L'assistant reste assez limité et la création personnalisée reste très simple donc préférer cette seconde solution

    2.CRÉATION PERSONNALISÉE

    La création d'un tableau croisé est particulièrement simple puisqu'il suffit de faire glisser les champs concernés en ligne, colonne avec les calculs à l'intersection.

     onglet "insertion"
    groupe "tableaux"     (1er bloc)
    une cellule de données du tableau étant sélectionnée
    <clic g>     sur
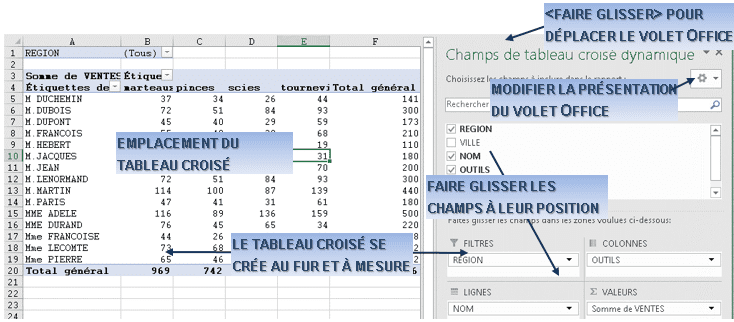
    vérifier     l’origine des données et l’emplacement de création du tableau croisé
     pour valider
    le volet "office" affiche la structure du tableau croisé
    faire glisser les champs à leur position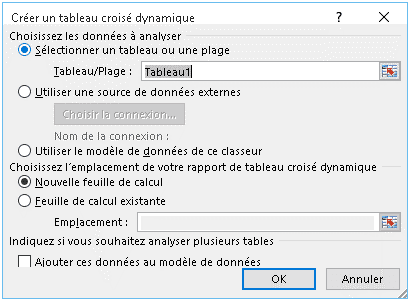

     Si la création du tableau croisé échoue, désactiver dans les options avancées :

     Modifier la présentation du volet "Office" en cliquant sur
    Le déplacer en le faisant glisser par sa barre de titre sur le document

    Le tableau est créé dynamiquement et offre une présentation synthétique et vivante des données au fur et à mesure du positionnement des champs.

     

     Ouvrir le classeur tabcrois.xlsx
    Créer à partir des données un tableau croisé permettant de lister les résultats par Région et par Nom
    (voir solution : tabcrois terminé.xlsx feuille "solution 1")

    3.MODIFICATION

    Un simple <clic g> dans le tableau croisé affiche sa structure dans le volet office ; toute modification est alors possible en temps réel.

     volet office
    décocher     les éléments à ne pas prendre en compte
     pour valider

     Pour n'afficher que les valeurs correspondant à certains critères des champs ligne ou colonnes, il faut afficher les valeurs avec   et décocher les valeurs autres

      coche toutes les valeurs et permet de les choisir

     Afficher le classeur tabcrois.xlsx
    Modifier le tableau croisé en affichant les ventes par Ville et par Produit
    (voir solution : tabcrois terminé.xlsx feuille "solution 2")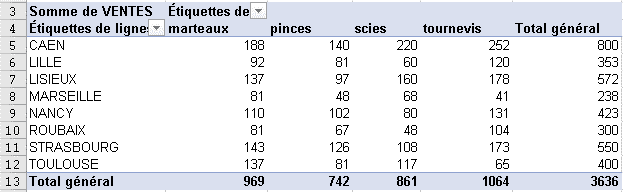

    4.CALCULS

    Une autre fonction que la somme peut être utilisée pour les champs de valeur.

    bouton droit
    dans le tableau croisé
    <clic d>     sur un champ de valeur
    <clic g> 
    choisir     le type de calcul

     pour valider

    bouton gauche
    dans le volet de structure du tableau
    <clic g>     sur   du champ de valeur
    <clic g> 
    choisir     le type de calcul
     pour valider

     Afficher le classeur tabcrois.xlsx
    Créer un tableau croisé de la moyenne des ventes par Région et par Produit
    (voir solution ; tabcrois terminé.xlsx feuille "solution 3")

    5.PRESENTATION

    La présentation du tableau croisé peut être optimisée, notamment en n'affichant plus les listes déroulantes de choix.

     onglet "analyse"
    groupe "afficher"     (dernier bloc)
    <clic g>  sur  pour ne plus les afficher

    B. GRAPHIQUES CROISES DYNAMIQUES

    Les graphiques croisés dynamiques sont créés de la même manière que les tableaux, aussi bien à partir d'une liste Excel que d'une base externe.

     onglet "insertion"
    groupe "graphiques"     (4ème bloc)
    une cellule de données étant sélectionnée
    <clic g>     sur   de
    choisir avec ou sans tableau
    confirmer     l’origine des données
    spécifier l’emplacement de création du graphique croisé
     pour valider
    le volet "office" affiche la structure du tableau croisé
    faire glisser les champs à leur position

     Pour intervertir les champs des axes, modifier dans le volet Office

     Afficher le classeur tabcrois.xlsx
    Créer un graphique croisé dynamique des ventes par Région et par Produit
    Repositionner et mettre en forme ce graphique
    (voir solution : tabcrois terminé.xlsx feuille "solution 4")

     Le filtre s'affiche en cliquant sur  de  et permet d'utiliser tous les opérateurs de comparaison texte ou numériques comme dans le "filtre automatique"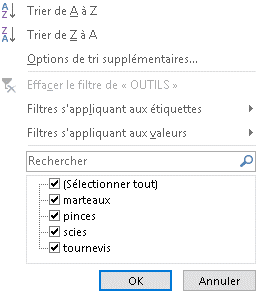

     

     Le tableau ou le graphique croisé dynamique peuvent être aussi créés de la même manière à partir de données externes

    C. CUBE OLAP

    Le cube Olap est une structure de base de données intelligente et pluridimensionnelle permettant de travailler sur une partie des données comme dans un sous-ensemble de la base.

    1.CRÉER UN TABLEAU CROISÉ

    Créer au préalable un tableau croisé dynamique puis transformer celui en cube olap.

     onglet "insertion"
    groupe "tableaux"     (1er bloc)
    une cellule de données du tableau étant sélectionnée
    <clic g>     sur
    vérifier     l’origine des données et l’emplacement de création du tableau croisé
     pour valider
    faire glisser les champs à leur position

     Ouvrir le classeur "ventes par catégorie et par exercice"
    Créer un tableau croisé avec les catégories en colonne

    2.TRANSFORMER EN CUBE OLAP

    Créer le cube, c'est créé un système de références en 3 dimensions.

     onglet "analyse"
    groupe "calcul"     (6ème bloc)
    <clic g> sur
    <clic g>     sur
    le tableau croisé est converti en cube olap

     Les contenus des cellules sont remplacés par une formule faisant référence à leur position dans le cube

     Dans le classeur "ventes par catégorie et par exercice"
    Transformer le tableau croisé en cube olap
    lui affecter une mise en forme simple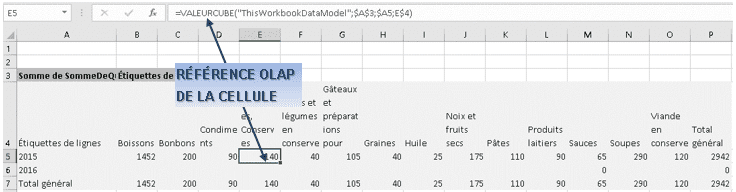

     Le cube olap ne peut recevoir de mise en forme de type "mettre sous forme de tableau"