Cours en ligne Excel 2010 gestion, finances, solveur
Résumé de section
-
L'éditeur d'équations est indispensable pour concrétiser des notions mathématiques. Il permet d'écrire toutes sortes d'équations en respectant les normes et usages.
 ACTION
ACTION onglet "insertion"
onglet "insertion"
groupe "symboles" (8ème bloc)<clic g> sur
 de
de  pour choisir une équation connue
pour choisir une équation connue
ou
<clic g> sur pour saisir l'équation
pour saisir l'équation
choisir une structure
saisir les valeurs
ajouter éventuellement des symbolesINSÉRER UNE STRUCTURE
 ACTION
ACTION onglet "CONCEPTION"
onglet "CONCEPTION"
groupe "structure" (3ème bloc)positionner le point d'insertion dans l'équation
<clic g> sur l'outil correspondant aux structures désirées
saisir les valeurs dans les zones prévues
INSÉRER UN SYMBOLE
 ACTION
ACTION onglet "CONCEPTION"
onglet "CONCEPTION"
groupe "symboles" (2ème bloc)positionner le point d'insertion dans l'équation
<clic g> sur le symbole exercice
exerciceDans la feuille "Région Est" du classeur "exercice graphique"
Insérer l'équation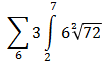 sous le tableau
sous le tableau -
Le plan va permettre de choisir le niveau d’agrégation des données.
 ACTION
ACTION bouton gauche
bouton gauche<clic g> sur le symbole voulu
SYMBOLES :
 développe (affiche) les niveaux de plan inférieurs
développe (affiche) les niveaux de plan inférieurs réduit (masque) les niveaux de plan inférieurs
réduit (masque) les niveaux de plan inférieurs affiche les 3 premiers niveaux de plan
affiche les 3 premiers niveaux de plan affiche les 2 premiers niveaux de plan
affiche les 2 premiers niveaux de plan affiche le premier niveau de plan
affiche le premier niveau de plan -
Les fonctions financières peuvent être très utiles dans les services administratifs, comptables ou financiers des entreprises.
1 LES INVESTISSEMENTS
Des fonctions spécifiques permettent de calculer des ratios très précieux dans l'évaluation de la rentabilité prévisible d'investissements.
FONCFIN.XLSX - TAUX-LN-NPM

a) =NPM(taux;versement;val._actuelle;val._capitalisée;type)
Cette fonction détermine le nombre de périodes nécessaires (années, trimestres, mois...) pour qu'une série de versements constants atteigne, en fonction d'un taux d'intérêt donné, une valeur capitalisée spécifiée.
 infos
infosType prend la valeur 0 pour des versements fin de période et 1 pour des versements début de période

b) =TAUX(nb_périodes;versement;val.actualisée;val.capitalisée;type)
Cette fonction calcule le taux d'intérêt qui permet à une somme investie (valeur actualisée) d'atteindre une valeur donnée (valeur capitalisée) en un nombre de périodes définis.
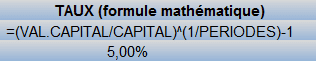
 exercice
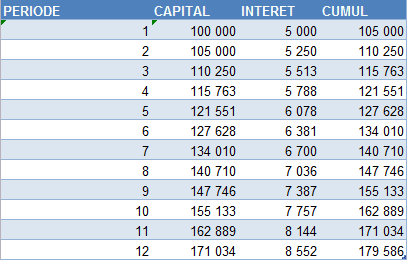
exerciceCalculer le nombre d'années nécessaires pour qu'une série de versements de 5 000€ atteigne, pour un taux d'intérêt de 5 % annuel, une valeur capitalisée de 100 000€
Calculer le taux d'intérêt qui permet à une somme investie de 100 000 € d'atteindre la valeur de 179 586 € en 12 annéesc) =TRI(ressources;taux estimé)
Cette fonction calcule le T.R.I (Taux de Rendement Interne) d'un investissement à partir des ressources nettes qu'il génère.
Le T.R.I. est la valeur prise par le taux d'actualisation (arg2 : taux estime) qui rend le total des ressources nettes générées pendant la période de référence (arg1 : ressources) égal au montant de l'investissement net initial.
 Il présente l'avantage d'être un ratio indépendant de l'environnement qui ne prend en compte que des données propres à l'investissement considéré ; il permet d'avoir un classement comparatif des investissements les uns par rapport aux autres et ce sans facteur exogène.
Il présente l'avantage d'être un ratio indépendant de l'environnement qui ne prend en compte que des données propres à l'investissement considéré ; il permet d'avoir un classement comparatif des investissements les uns par rapport aux autres et ce sans facteur exogène. Il présente l'inconvénient de ne pas permettre de faire de distinction en fonction de l'importance des capitaux investis ni en fonction des périodes de vie des investissements.
Il présente l'inconvénient de ne pas permettre de faire de distinction en fonction de l'importance des capitaux investis ni en fonction des périodes de vie des investissements. Plus le T.R.I. est élevé, plus l'investissement est rentable.
Plus le T.R.I. est élevé, plus l'investissement est rentable.
 exercice
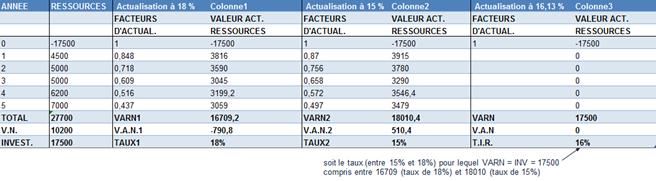
exerciceQuel est le TRI d'un investissement de 17 500 € générant 4 500 € la 1ère année, 5 000 € la deuxième, 5 000 € la troisième, 6 200 € la quatrième et 7 000 € la cinquième
FONCFIN.XLSX - TRI-VAN
d) =TRIM(Valeurs;taux financemt CF;taux placement CF)
Cette fonction calcule le Taux de Rendement Interne Modifié d'une série de Cash-flows périodiques. Il prend en compte le coût du financement des cash-flows et l'intérêt perçu sur leur placement.
e) =VA(taux;nbre_périodes;versement;type)
Cette fonction permet de connaître la valeur, en francs actuels, d'une série de versements constants placés à un taux d'intérêt défini. Elle ramène une somme en francs futurs à sa valeur actuelle à des fins de comparaison. Elle peut ainsi permettre de faire la comparaison entre une rente périodique et une somme cash.
FONCFIN.XLSX - VA


 exercice
exerciceQuelle est la valeur actualisée d'un versement annuel de 5 000 € en début de période pendant 12 ans
f) =VAN(taux;ressources)
Cette fonction permet de calculer la valeur actualisée nette des ressources générées par un investissement, ceci à un taux d'intérêt constant (ou encore la valeur actualisée de l'investissement lui-même en incluant la dépense initiale).

 exercice
exerciceQuel est la valeur actualisée nette de revenus de 4 500 € la 1ère année, 5 000 € la deuxième, 5 000 € la troisième, 6 200 € la quatrième et 7 000 € la cinquième, à un taux de 18%
g) =VC(taux;nbre_périodes;versement;valeur_actuelle;type)
Cette fonction calcule la valeur capitalisée d'une série de versements égaux effectués à un taux d'intérêt constant pendant n périodes. Type prend les mêmes valeurs que précédemment.

 exercice
exerciceUne société épargne tous les ans 5000 € versés en une seule fois en début de période et placés à un taux fixe de 4,3 %.
Calculer la valeur capitalisée de ces versements au bout de 12 ans
Idem mais avec des versements fin de période.
Calculer la valeur actualisée si au lieu de versements constants, l’ensemble du capital était investi en une seule fois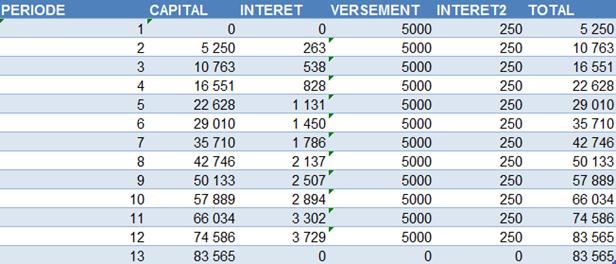
2 LES EMPRUNTS
Les emprunts, de la même façon que les investissements, peuvent être calculés avec les fonctions Excel.
FONCFIN.XLS - VPM-INTPER-PRINCPER

a) =INTPER(taux;Nopériode;périodes;val.actualisée;val.capitalisée;type)
Cette fonction permet de calculer le montant des intérêts payés sur une période donnée dans un plan de remboursement d'emprunt.
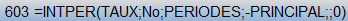
b) =PRINCPER(taux;No_période;périodes;valeur_actualisée;valeur_capitalisée;type)
Cette fonction permet de calculer le montant du capital remboursé sur une période donnée dans un plan de remboursement d'emprunt.
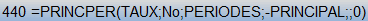
c) =VPM(taux;périodes;val.actualisée;val.capitalisée;type)
Cette fonction permet de calculer les versements nécessaires au remboursement d'un emprunt en fonction du nombre de périodes de remboursement et du taux.
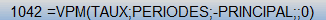
 exercice
exerciceVous empruntez pour acheter une maison la somme de 150 000 € au taux de 5 % par an, assurances comprises et ce sur 18 ans.
Sachant que les intérêts d’une mensualité s’exercent sur le capital restant dû (moins celui déjà remboursé), faire un tableau de remboursement mensuel décomposant intérêts et capital
Calculer la mensualité de remboursement avec la fonction Excel appropriéeFONCFIN.XLSX - VPM-INTPER-PRINCPER

3 LES AMORTISSEMENTS
La notion d'amortissement d'Excel est une notion économique qui prend en compte la valeur de revente des immobilisations. Cependant, une utilisation selon les préceptes du plan comptable général, amène à des calculs d'amortissement comptable.
 infos
infosL'amortissement comptable doit, en FRANCE, se pratiquer sur la totalité de la valeur d'achat, indépendamment d'une éventuelle valeur de revente et en prenant en compte, non pas la durée d'utilisation mais la durée légale d'amortissement. Les fonctions suivantes vont donc surtout trouver leur utilité dans les services de gestion pour effectuer des simulations, des prévisions ou encore pour obtenir une comptabilité analytique plus proche de la réalité économique que la comptabilité générale
AMOS.XLS
a) =AMORLIN(coût;valeur_résiduelle_durée)
Cette fonction calcule l'amortissement d'une immobilisation en mode linéaire.

b) =DB(coût;valeur_récupération;durée;période;mois)
Cette fonction calcule, pour une période donnée, la dépréciation d'un amortissement selon la méthode américaine de l'amortissement décroissant.
c) =DDB(coût;valeur_récupération;durée;période;facteur)
Cette fonction calcule, pour une période donnée, l'annuité d'amortissement dégressif d'une immobilisation en fonction de sa valeur d'achat, de son éventuelle valeur de revente et de sa durée d'amortissement.
 infos
infosFacteur est le taux auquel le solde à amortir décroît. s'il n'est pas indiqué, 2 est pris par défaut

d) =SYD(coût;valeur-recupération;durée;période)
Cette fonction calcule, pour une période donnée, la charge d'amortissement d'une immobilisation selon le mode "Sum of years digit américain".

e) =VDB(coût;val.récupération;durée;pér_début; pér_fin)
Cette fonction calcule l'amortissement d'un bien selon la méthode Variable Declining Balance.

 exercice
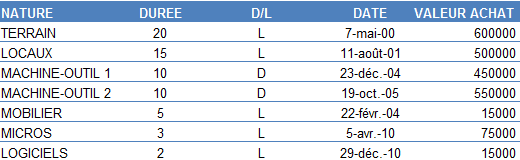
exerciceUne entreprise achète les biens suivants :
Un terrain le 07 mai 2000 pour 600 000 € ; elle y fait construire des locaux le 11 aout 1999 pour 500 000 €
Une machine-outil le 23 décembre 2004 pour 450 000 €
Une seconde machine-outil le 19 octobre 2005 pour 550 000 €
Du mobilier le 22 février 2004 pour 15 000 €
Des micro-ordinateurs le 05 avril 2010 pour 75 000 €
Des logiciels le 29 décembre 2010 pour 15 000 €
Calculer la valeur annuelle des amortissements de chaque bien